Skip to main content

How a Force vs. Time Graph Helps You Calculate Impulse, Momentum, and Velocity

airbag impulse momentum theorem example
Credit: Public Domain

By Andrew Bennett

The momentum of an object is the product of its mass and its velocity. A force must act on an object to change its momentum. The size of the force and the time over which that force acts both determine how much the momentum changes. In fact, the product of the force and the time are exactly equal to the change in momentum of the object. This product is called the "impulse delivered by the force."

Impulse-Momentum Theorem and Newton's Second Law

Newton's 2nd Law Definition

Newton's 2nd law says that the acceleration of an object (a) is equal to the force on it (F) divided by its mass (m), or:

Force vs. Time Graph Impulse Momentum Velocity.

The acceleration of the object can be calculated as the change in its velocity over the change in time, so we can replace acceleration in the equation above and get:

Force vs. Time Graph Impulse Momentum Velocity.


Multiplying both sides by mass and by time gives the result:

Force vs. Time Graph Impulse Momentum Velocity.

With the product of mass and velocity in that equation, it begins to look like a momentum calculation.

Impulse-Momentum Theorem Definition

The mass times the change in velocity of an object is the same as the change in momentum of that object, so we can rewrite the previous equation as:

Force vs. Time Graph Impulse Momentum Velocity.

The force on an object multiplied by the amount of time the force acts is equal to the change in momentum of the object. Impulse is defined as the force on an object multiplied by the time over which that force acts.

The Impulse-Momentum Theorem states that the impulse delivered to an object or system is equal to its change in momentum. One common case, which we'll address in the "conservation of momentum" post, is when there is no force acting on a system. In this case, the change in momentum will be zero, meaning that the total momentum of the system does not change.

Solving Impulse-Momentum Problems

Our first video on this topic further explains the relationship between Newton's 2nd Law and the Impulse-Momentum Theorem. We then apply the equation to an example problem involving a car applying its brakes to find its new velocity.


What Is a Force vs. Time Graph?

When the force is constant, we can calculate impulse by simply multiplying force by time. Yet in some cases, the force is changing. We can't just pick one value of the force to multiply by time. 

The solution is a very basic form of calculus. If you're not a fan of calculus, don't worry. You only need to find the area of triangles and rectangles.

When force changes over time, we can calculate impulse by graphing force vs. time. We will then calculate the area between our graphed values and the X-axis. Typically, this is called the "area under the curve," but the graph doesn't have to be curved. The area might actually be "over the curve" if we have negative values for force.

Using a Force vs. Time Graph to Find Velocity and Momentum 

After we find a value for impulse, we can calculate new values for momentum or velocity. We can do this because impulse is equal to the change in momentum. 

In our second video, we work through a force vs. time graph calculation to find impulse. Then, we use that value to calculate the change in momentum.


More Physics Videos

For more information on this topic, check out the other videos in this momentum playlist and subscribe to my YouTube channel.

Labels:

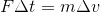
Comments

Post a Comment

Popular posts from this blog

Why Do They Do That? The Physics Behind 3 Famous Animal Behaviors

By Amber Bennett Have you ever wondered about the origins of the phrase, "get your ducks in a row"? What about how the "doggy paddle" works or why squirrels are such amazing jumpers? The answers to all of these questions have one thing in common: physics. Keep reading to learn about the science behind these three famous animal behaviors. How Do Squirrels Leap from Branch to Branch? A squirrel leaps through the air.  Photo Credit:  caroline legg ,  CC BY 2.0 , via  Wikimedia Commons The death-defying acrobatic maneuvers performed by squirrels look a lot like parkour tricks. But how do they know how to land tricky jumps between bendy tree branches that move with the wind?  Researchers say  it's a combination of learned behavior (practice makes perfect) and inherited adaptations.  To see what determines how far a squirrel is willing to jump and how the leaps are timed, researchers set up an obstacle course in an artificial forest. Then, they used peanuts ...
Post a Comment
Read more

3 Easy Science Experiments to Do with Your Kids

By Amber Bennett Strong STEM (science, technology, engineering, and math) skills set kids up to succeed both in school and later in life. Encouraging them to be interested in these subjects is easier than you might think, especially if you start when they're young.  Activities that encourage children to be curious and creative will spark a love of learning. Plus, science experiments and other hands-on STEM projects are a fun way to bond with your kids. Here are three easy science experiments that preschoolers and early elementary students will enjoy. 1. Leakproof Plastic Bag A (age 5) doing the leakproof plastic bag experiment. Our preschooler loves to do any experiment that involves water. I can give her a couple of beakers, and she'll happily pour water back and forth between them, especially if I put a few drops of food coloring in each beaker so she can mix the colors.  Another great activity that involves water is the leakproof plastic bag.  All you need are: Large p...
Post a Comment
Read more

How Virtual Currency Mining Is Hurting the Environment - Science in the News

Datacenters used for cryptocurrency mining use a lot of energy. By Amber Bennett Although cryptocurrencies are virtual, they are having a tangible impact on our environment. Research shows that cryptocurrencies actually are worse for the earth than other types of money. So, why is that? Simply put, it's because of the resources needed to run the supercomputers that mine Bitcoin and other virtual currencies.  Energy Use The datacenters used for mining use large amounts of electricity. For example, the global Bitcoin network uses  more energy than entire countries . In fact, according to the University of Cambridge Bitcoin Electricity Consumption Index , the network's power demand is the same as more than 14 million typical American homes. Most of the energy used in the datacenters comes from fossil fuels instead of renewable resources. Plus, datacenters' high energy use can destabilize the electric grid. Materials Mining Another way that cryptocurrency impacts the environme...
Post a Comment
Read more