 |
| Credit: Public Domain |
Collisions between objects are often treated using the conservation of momentum in physics. Energy can be tricky to deal with. We frequently have some amount of mechanical energy turning to nonmechanical energy, and it's difficult to predict how much. The collision causes atoms within the objects to shake, meaning they have kinetic energy (but we call it thermal energy when it's for individual atoms). This has taken away from the kinetic energy of the objects as a whole. It is not always clear how much of the original kinetic energy the objects will have after the collision. There is no such concern with momentum, so it is a useful way to understand these situations.
Strictly speaking, this doesn't actually happen with large objects. Sometimes it's really close, like when two billiard balls collide. This is only seen exactly in cases of collisions between subatomic particles, but we'll get to that later.
With elastic collisions, we write an equation saying that the total initial momentum is equal to the final momentum.
However, we also write an equation saying that the initial total kinetic energy is equal to the final kinetic energy.
This can make for some tricky-to-solve practice problems with systems of equations, as is shown in the video below.
The only time we might consider energy here is if a problem specifically asks, "How much kinetic energy turns to thermal energy during this collision?"
In a completely inelastic collision, there is no bouncing off at all. The objects move together after the collision. Examples include a bullet hitting a block of wood and becoming embedded in the wood and a football player tackling another and holding onto them as they fall.
Again, we can't do any useful calculations with energy. However, we know that the objects move together after the collision. So, they can be treated as one big object (a "combined mass") in that moment. In a situation where two objects (labeled A and B respectively) collide and stick together, we could write an equation for the conservation of momentum during the collision as
or, expanded by substituting the equation for momentum in each term,
Classes of Collisions
However, we need to know about a few classes of collisions. The classes are divided up according to what is happening with energy in a particular situation. The classes are called elastic collisions, inelastic collisions, and completely (or totally) inelastic collisions.Elastic Collision Definition
In an elastic collision, the objects that collide have just as much kinetic energy after the collision as they did before. None of that energy turns to thermal energy.Strictly speaking, this doesn't actually happen with large objects. Sometimes it's really close, like when two billiard balls collide. This is only seen exactly in cases of collisions between subatomic particles, but we'll get to that later.
With elastic collisions, we write an equation saying that the total initial momentum is equal to the final momentum.
However, we also write an equation saying that the initial total kinetic energy is equal to the final kinetic energy.
This can make for some tricky-to-solve practice problems with systems of equations, as is shown in the video below.
Inelastic Collision Definition
Inelastic collisions are the general, run-of-the-mill type. Some kinetic energy turns to thermal, but we don't know how much. We can't do anything useful by thinking about kinetic energy, so we just do the conservation of momentum equation.
Or, expanded in the example of a two-object collision,
Completely Inelastic Collision Definition
In completely inelastic collisions, kinetic energy turns to thermal energy. There is an upper limit of how much kinetic energy can turn to thermal. When very little energy changes, the objects bounce off each other quite well. As more and more energy changes from kinetic to thermal, the bouncing effect is reduced.In a completely inelastic collision, there is no bouncing off at all. The objects move together after the collision. Examples include a bullet hitting a block of wood and becoming embedded in the wood and a football player tackling another and holding onto them as they fall.
Again, we can't do any useful calculations with energy. However, we know that the objects move together after the collision. So, they can be treated as one big object (a "combined mass") in that moment. In a situation where two objects (labeled A and B respectively) collide and stick together, we could write an equation for the conservation of momentum during the collision as
or, expanded by substituting the equation for momentum in each term,



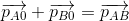
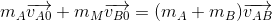
Comments
Post a Comment