 |
| Photo Credit: Public Domain |
By Andrew Bennett
Fluids in motion show some interesting properties. In fact, some behaviors are so far impossible to predict exactly. In a first-year high school physics class, we tend to limit our discussion of moving fluids to the simpler cases, involving incompressible, nonviscous fluids with consistent flow rates. Water moving through pipes is a great example of this, so we end up doing a lot of problems about water in pipes of different shapes and sizes.
This idea can be expressed by the continuity equation, which reads:
The product of the cross-sectional area and the fluid speed is equal to the "volume flow rate" of the water, which tells what volume of water moves through a part of the pipe per unit of time. (You might see numbers in gallons per minute or similar units for certain appliances; this is a volume flow rate.) Making the assumptions described earlier, we find that the volume flow rate must be consistent throughout the pipe, leading to the continuity equation above.
We've looked at the conservation of energy before. With the possibility for work input and output, we can write the conservation of energy equation as:
That's all the Bernouli equation is. On each side of the equation, we typically write this out with three terms: one related to work, one for kinetic energy, and one for gravitational potential energy. If we put in the equation for the work and for each energy type, then divide all terms by the volume, we get the Bernouli equation.
In the video below, I'll take you through that derivation, so you'll understand where each term comes from and how to plug in values appropriately to learn about the pressure, speed, and height of a fluid.
Continuity Equation and Volume Flow Rate
With these assumptions, we can conclude that in some amount of time, the same amount of water must pass one point in the pipe as passes another nearby point in the pipe. If anything else were true, we would have water appearing or disappearing between the two points.This idea can be expressed by the continuity equation, which reads:
The product of the cross-sectional area and the fluid speed is equal to the "volume flow rate" of the water, which tells what volume of water moves through a part of the pipe per unit of time. (You might see numbers in gallons per minute or similar units for certain appliances; this is a volume flow rate.) Making the assumptions described earlier, we find that the volume flow rate must be consistent throughout the pipe, leading to the continuity equation above.
Flow Rate of Air
It is worth noting that this does not apply for compressible fluids, such as air. Air, being compressible, can be made to take up less space or more space (that is, to change volume). If the volume of the air can change over time, there is no reason to expect the volume flow rate to remain constant.
If viewing via email, click here to watch the video.
What Is the Bernouli Equation?
The Bernouli equation is widely applicable to a wide range of moving fluid situations. (Be sure to go tell someone you've been learning about "fluid dynamics" today - it sounds very impressive!) We will often use this in situations like we saw with the continuity equation, such as water moving through pipes. This is simply so that we can use both the continuity equation and this new Bernouli equation in the same problem. No such conditions are required for the Bernouli equation to work.We've looked at the conservation of energy before. With the possibility for work input and output, we can write the conservation of energy equation as:
That's all the Bernouli equation is. On each side of the equation, we typically write this out with three terms: one related to work, one for kinetic energy, and one for gravitational potential energy. If we put in the equation for the work and for each energy type, then divide all terms by the volume, we get the Bernouli equation.
In the video below, I'll take you through that derivation, so you'll understand where each term comes from and how to plug in values appropriately to learn about the pressure, speed, and height of a fluid.
If viewing via email, click here to watch the video.

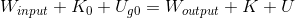

Comments
Post a Comment