Image Credit: Wikimedia Commons
As I'm using radians as my unit of measure for all angles in my Cavendish experiment, I thought some background might be useful for some of my readers. So, let's get right to it.
Instead, if we had walked along the outside of the circle for a distance equal to 2 times the radius, then the lines we drew would have had an angle between them equal to 2 radians.
Walking all the way around the outside of the circle would be roughly equal to 6.28 times the radius, so the angle for one complete revolution is about 6.28 radians, too.
It gets stranger. If you wanted to describe an angle less than 1 degree, the convention is to tell how many minutes of arc the angle is. Sixty minutes of arc is equal to 1 degree. One full revolution is the same, then, as 60 x 360 — or 21,600 minutes of arc.
If the angle was smaller than 1 minute of arc, you'd go to seconds of arc. Sixty seconds of arc is the same as 1 minute of arc, and 3,600 seconds of arc is the same as 1 degree, and one revolution is equivalent to 1,296,000 seconds of arc.
All the 60s here seem to be a carryover from the Babylonians, who used a base 60 number system. There is also reason to believe that the Babylonians derived what they knew about the circle by circumscribing the circle in a hexagon, which can then be divided into six triangles, which were each assigned an angle of 60 (6 x 60 gets us to the 360 degrees for the full circle). We've kept up the practice simply out of habit, I suppose, despite our base 10 number system.
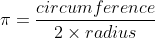
Solving for circumference gets us the equation:
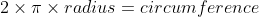
The angle we've walked through as we walk around the circle is equal to how many radiuses of distance we've traveled. If we walked the circumference of the circle, we would have gone through an angle of 2 pi radians. So one revolution, which is 360 degrees in one system, can also be described as 2 pi radians.
The convention for smaller angles is frequently to use fractions that include pi. Half a rotation would be equal to pi radians. One-fourth of a revolution would be the same as pi/2 radians, and so on.
What Is a Radian?
Simply put, a radian is a unit for measuring angles. Imagine a big circle drawn on the ground in chalk. Use your chalk to draw a straight line from the center of the circle to the edge, and measure that line (the radius of the circle). Now, walk that same distance around the outside of the circle (if the circle has a radius of 5 meters, walk for 5 meters on the edge). Draw a new line from the edge of the circle where you are standing back to the middle. The two lines you've drawn have an angle between them that we define to be equal to 1 radian.Instead, if we had walked along the outside of the circle for a distance equal to 2 times the radius, then the lines we drew would have had an angle between them equal to 2 radians.
Walking all the way around the outside of the circle would be roughly equal to 6.28 times the radius, so the angle for one complete revolution is about 6.28 radians, too.
What Is a Degree?
Many of us are more familiar with the degree as an angle unit. A degree is 1/360th of the full rotation around a circle. Although degrees might seem less intimidating because you've used them more, you have to admit that they seem a bit arbitrary, right? Why is 360 degrees the same as one revolution?It gets stranger. If you wanted to describe an angle less than 1 degree, the convention is to tell how many minutes of arc the angle is. Sixty minutes of arc is equal to 1 degree. One full revolution is the same, then, as 60 x 360 — or 21,600 minutes of arc.
If the angle was smaller than 1 minute of arc, you'd go to seconds of arc. Sixty seconds of arc is the same as 1 minute of arc, and 3,600 seconds of arc is the same as 1 degree, and one revolution is equivalent to 1,296,000 seconds of arc.
All the 60s here seem to be a carryover from the Babylonians, who used a base 60 number system. There is also reason to believe that the Babylonians derived what they knew about the circle by circumscribing the circle in a hexagon, which can then be divided into six triangles, which were each assigned an angle of 60 (6 x 60 gets us to the 360 degrees for the full circle). We've kept up the practice simply out of habit, I suppose, despite our base 10 number system.
Where Does Pi Come in?
Pi is defined as the ratio of a circle's circumference to its diameter. Since the diameter is twice the radius, we could also say that pi is equal to the circumference of a circle divided by two times the radius.Solving for circumference gets us the equation:
The angle we've walked through as we walk around the circle is equal to how many radiuses of distance we've traveled. If we walked the circumference of the circle, we would have gone through an angle of 2 pi radians. So one revolution, which is 360 degrees in one system, can also be described as 2 pi radians.
The convention for smaller angles is frequently to use fractions that include pi. Half a rotation would be equal to pi radians. One-fourth of a revolution would be the same as pi/2 radians, and so on.
Image Credit: Wikibooks
What Is an Arc Length?
When looking at two points on a curved line, the arc length is the distance between them along the circle. One great thing about radians is that arc length is extremely easy to calculate if you know the angle between the points. The angle in radians is simply multiplied by the radius of the circle, or:
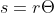
where s is the arc length, r is the radius, and theta is the angle in radians.
where s is the arc length, r is the radius, and theta is the angle in radians.
Video: An Intro to Radians and More
In this video, I'll show you how a radian is defined and what makes it such a useful unit.
If viewing via email, click here to watch the video.
Stay Tuned to Learn How This Is Related to My Cavendish Experiment
The fact that we can easily use angles in radians to find arc lengths will be of importance in the next Cavendish video. Be sure to subscribe, so you don't miss that one!


Comments
Post a Comment